Wrap Your Brain Around Monty Hall
NOTE: this post also appears on the wonderful site about crazy coincidence, theoddsmustbecrazy.com.
I have always been amused and intrigued by responses to “The Monty Hall Problem”, especially when I talk about it to audiences with a high concentration of engineers and mathematicians. If you are familiar with it, but you’ve always struggled with an unsettled feeling of “this can’t be right”, read further and let me know if my explanation of the solution helps to alleviate the discomfort. If you are not familiar, I guarantee you will give your brain a workout by reading on.
First posed to statisticians in 1975, “The Monty Hall Problem” is well-known among academics because it still sparks debate. Many seem to think that disagreements about its solution stem from issues in the clarity of the problem, but I contend that it really stems from human flaws in the way that we process information.
I often discuss this problem in statistics and cognitive psychology courses for several reasons. It is a great exercise in probability calculation and it can be used to teach basic mathematical modeling (and its purpose). An added benefit, since almost all of my students were psychology majors, is that it also illustrates a flaw in human cognition as well as a pattern of problem solving. Even a knowledgeable statistician feels the need to run simulations to see the solution in action. Even then, fully grasping the mechanisms behind the answer often requires brute force cognition.
In general, human beings have a very difficult time wrapping their brains around concepts of probability. It is much like a visual illusion; we know that the lines are parallel/the circles are the same size/there is no motion, but we can’t make our brains process it in a way that represents that reality. It’s just not how our visual system works. I hypothesize that one of the reasons that probability is such a difficult field for most people is that it involves theory and models, which are distinct from observations and we must represent them differently in our minds to properly deal with them. Applications of probability often involve switching gears from the realm of models to data or vice versa and this is where I think most mathematicians get side-swiped in The Monty Hall Problem.
The Poser
In essence, here’s the problem:
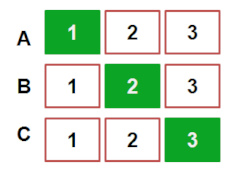
You are a contestant on Let’s Make a Deal!and Monty loves your creative costume (a teddy bear carrying a human doll), so he calls on you to make a deal. Monty says, “There are three doors – Door #1, Door #2, and Door #3. Pick one and you get to keep whatever is behind it.”You’ve seen the show (you weren’t just walking down Ventura Boulevard in a teddy bear costume for fun), so you know that it is highly likely that there is a coveted BRAND NEW CAR! behind one of those three doors. If you choose wrong, however, you might end up with an ostrich…
You choose Door #3.
Monty then says, “Let’s see what’s behind Door #1!” and the door opens to reveal one of the many consolation prizes (and product placements), a lifetime supply of Rice a la Roly.
Cool! You might get that car after all!
Well, the show was successful because the shell-game-huckster-style of Monty Hall rarely stopped there. In this case, he does what he often does, offers to let you switch from your first choice (Door #3) to the only remaining option, Door #2.
Should you? Does it matter?
Not the Problem
Before I get into the solution, let me first deflect a common complaint from mathematicians. The most well-known version of the problem, from its Wikipedia entry:
Suppose you’re on a game show, and you’re given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1 [but the door is not opened], and the host, who knows what’s behind the doors, opens another door, say No. 3, which has a goat. He then says to you, “Do you want to pick door No. 2?” Is it to your advantage to switch your choice?
This version does not specifically state the name of the show or indicate the way that game shows of its era worked. If you have never seen the television show (i.e., you are younger than 35), or any game show of its kind, let me explain. Monty is in control of almost everything that happens. The only thing “contestants” can do is make choices when Monty offers them. As you will see, they had more control over their odds of winning than once thought, but Monty manipulates some of the build-up by choosing which items to reveal at different steps in the game.
Unfortunately, many probability theorists and mathematicians took issue with the lack of clarity in the problem (context is important sometimes). This provides a face-saving ‘other version’ for the geeks who get it wrong the first time. But whenever I hear comments like, “Okay, given this version, that Monty knows where the car is.” I usually think, “Of COURSE he knows where the car is! There is no other way to play the game!” and wish that people were more able to accept that they are just as human as everyone else.
The problem itself is written clearly, though: it specifically states that a door without a car behind it is revealed before you are given the option to switch. If the situation was a fully-randomized, double-blind game (like “Deal or No Deal”), then the option to switch would not even be on the table if the car is behind the revealed door. There would be no problem in that case. Therefore, the problem is a question of whether you should switch in a controlled setting – one in which the only participant who doesn’t know the location of the big prize is you.
The issue of knowledge is a factor in our processing of the problem, but it’s not what Monty knows that matters. It’s what you (the subject of the problem) know.
So, let’s put that complaint behind us and get back to the problem.
The Answer, and How to See it for Yourself
Hopefully, if the problem is new to you, you’ve spent some time trying to solve it instead of going with your first gut feeling, which was probably, “It doesn’t matter.”
It does. You should switch.
If you don’t believe me, try running some simulations. You’ll have to run a lot in order to get a large enough sample to be certain to see the trend, but here are a few ways to do it:
- Use your favorite program (MATLAB, R, etc.). There is a good database of pre-written simulators for this here. I am partial to Excel myself, even though it’s a bit more cumbersome. I just don’t remember enough code to use another program.
- Use a web-based simulator. Do it at least a hundred times, choosing to switch for half of the trials, and keep a tally your results.
- Use a die to simulate the outcome, assigning 1-3 to “Door #2″ and 4-6 to “Door #3″ (e.g., if you roll a 5, Door #3 is the one with the car). Roll at least a hundred times, choosing to switch for half of the trials (before rolling!). Keep a tally of the results.
What you will see is that switching will result in winning a car in approximately 2/3rd of the trials while staying will only provide a win in 1/3rd of them.
I know what you’re thinking. “But, there are only two doors left, so it should be 50/50!”
Why it is so Difficult to Accept
Human cognitive development is an interesting process. We learn to interpret information from the environment very quickly so that we can respond to that environment, but learning to reason hypothetically takes more time. Even adults with scientific training have a difficult time separating the concept of variables (each has a set of possible values) and data (values which are known).
In practice, hypothetical situations are often conditional (e.g., “If A, then B”). We tend to use information about what is to reason about what could be. We do this because it often works, but it is one of the ways in which our brains can lead us astray. For example, given the premise, “If I study, I will get a good grade on the exam”, what is the most sound conclusion when presented with a good grade? The most common response is, “I must have studied”, but that is not sound. In this premise, studying provides a guarantee for a good grade, but there is no statement that studying is the only way to get a good grade. It does not, for example, read, “If and only if I study…”
In the case of the Monty Hall Problem, the probability of winning is set before you pick a door. No matter which door you choose, the probability is 1/3rd. This is because there is a 1/3rd probability that the car is behind the door you chose given the information you had when you chose it. In reality, the car is behind one of the doors, so the probability it is behind Door #2 is 100% if it is there and 0% if it is not there. Probability is not a useful way to discuss what is or what happened; it is a tool for predicting what is likely to be true/happen.
The new information provided by revealing a loser changes the circumstances and this where we get trapped in our representations of models and data, possibilities and facts.
You had a 1/3rd chance of winning because there were three, equally-likely locations to choose from. It seems as if cutting the choice down to two should change the odds of winning to 1/2. It seems that way because we are focused on the probability that a given piece of information is true (e.g., that the car is behind Door #1) and not the probability that an event will occur (e.g., that we will win the car). The probability that we will win the car relies on the number of possible states of reality. This, in turn, initially relies on the number of locations for the car. When the situation changes, we try to adjust probabilities based on possible locations (which has changed) rather than on the number of possible states of reality (which has not).
Basically, when Monty makes the second offer, the offer is to switch from the door we have (#3) to the door we don’t have (#1 or #2). It does not matter that only one of those doors is left; there is still only a 1/3rd chance that our door has the car and a 2/3rd chance that the set of the other two contains the car.
Getting Un-Stuck
If you change the way you represent the problem from the beginning, the solution might seem more reasonable. Specifically, instead of thinking in terms of assigning probabilities to doors, think in terms of assigning probabilities to outcomes: winning verses losing.
Let’s go step by step…
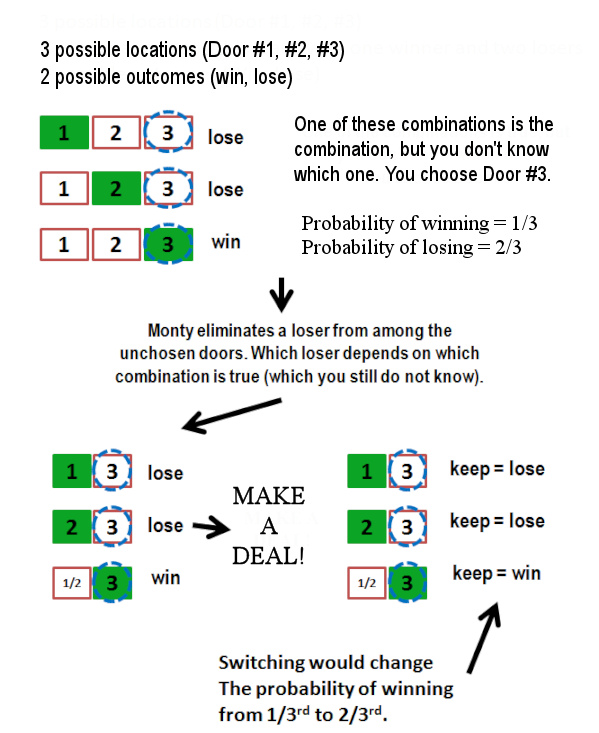
Monty asks you to pick a door from three choices. Behind one of those doors is a car. There are three possible locations and it must be in one of them, so there are three possible states of reality.
You choose to bet on Door #3; there is a 1/3rd chance that you will win the car.
There is a 2/3rd chance that you will not win the car.
This would be true no matter which door you chose.
Monty reveals that one of the remaining doors is a loser. At least one will be a loser since there is only one winner and you can choose only one. The car, however, does not move. Even though there are only two locations left, so there are still three possible states of reality. What’s changed is that we now know more about each of those possible states (there are fewer locations for the car to be):
So, if we model the problem in terms of the probability of winning with Door #3, the model itself does not change after the losing door is revealed. What changes is that we would no longer want to choose that door, so it is no longer among our options. This leaves us with only two options: keep the door we have or switch to the remaining door. The odds of winning/losing with Door #3 have not changed, but eliminating an option allows us to make a better choice – switch.







I’ve never been able to wrap my head around this one. I’ve been trying to find a better explanation than the usual ones out there, and I appreciate you presenting a very good one here …. but I still can’t comprehend it. I tried my own variation: Instead of 3 doors there are 103. I pick 1. Instead of revealing 1 donkey Monty reveals 101, and … I still don’t get it. I accept you are correct because enough people have run simulations 100,000 times, all with the same result. I think it all comes down to I can’t comprehend how the odds don’t change after I have more information – the door Monty revealed. I must be missing that particular neuron, or synapse or something (among many others). Next up: I flip a coin 10 times, the first 9 are tails. What are the odds the 10th flip will be heads? 50%? No? Yes? I’m ok though, I accept that there are many things I will never truly understand.
I don’t think you should assume that you’re deficient in any way. Most likely, you simply have yet to frame it properly so that you’re comfortable.
The coin flipping problem is a matter of separating dependent trials from independent trials. If the coin is fair, then it does not matter how many times it comes up tails, the probability is always 50% – the coin has no memory of previous trials.
But the Monty Hall problem is entirely different. Let me give it one more try, emphasizing one part of the post:
The probabilities you should be considering are not the probability that the car will be behind door #1, door #2, or door #3, but rather the probability that it will be behind the door you chose or a different door. Written as sets:
The way we think of it: {door #1 (1/3), door #2 (1/3), door #3 (1/3)}
The way it is: {chosen door (1/3), another door (2/3)}
When we are asked if we want to switch, we’re switching to “another door”, not a specific door. The problem is framed in a way that tricks us into thinking of it as switching to a specific door.
Did that make a difference?
I worked on this hard for about an hour, then went off to something else for a distraction, came back, refocused, worked on it some more. Then I slept on it, and tried again fresh in the morning. I’m still stuck on the same thing I’ve been stuck on for years, which I think is the same sticking point for many people: I can’t see how being given additional information after the process starts – the opening of one of the doors – doesn’t change the odds, especially since I have the option to make another move before the final reveal. At this point, I have your explanation memorized, I believe it (because of the simulations people have run), and I would get the answer correct if it was/were (another thing I struggle with) on a test, but I still don’t understand it. I usually visualize things when I try to solve them, and I can’t visualize this one. I need to set this aside for a while, else by repeating it too many times I might think I understand it, but not really understand it. Sometimes these things just spontaneously click for me and then they seem so simple. I will probably return to it in the future. I do appreciate your effort and attention and help with this.
I think the best explanation is seen in comments like the one by Jay posted yesterday afternoon. When you pick a door, that door has a 1/3 probability of winning. The collective set of all other doors that you did not pick has a 2/3 chance that at least one is the winning door. As doors are revealed, the probability of the one you picked doesn’t change because its probability was based on how many doors were available at the time you picked it. Therefore, all of the remaining doors combined still retain a 2/3 chance, but the revealed doors have added information about the set overall. If I open one, the 2/3 chance now belongs to the only unopened door among those two. I’m now left with a choice between my original pick at 1/3 or switching to a door with 2/3, so it is a safer bet to switch.
At the other posting on OddsMustBeCrazy, I put this comment as an alternate way of explaining the problem:
There is still another issue with the over-simplification of the Monty Hall Problem (without actually stating the assumptions used to simplify) which I also addressed at OddsMustBeCrazy, but assuming the simplistic version it really does give better odds to switch.
BTW, MythBusters looked at the Monty Hall Problem in an episode that aired last November. Watch It Here!
That’s a good “alternative game” that is equivalent to the extent the deck would have only 3 cards in it.
But, unlike Barbara’s reluctance to think more choices initially doesn’t clarify things by making being wrong initially quite obviously likely, I think this helps (like in my twisted lottery example) but it is better than mine because nearly everyone can relate to picking a card from a deck especially when using the “ace of spades” as the psychologically attractive prize marker. No strange alternatives of familiar processes are required unlike in my lottery style game. Nice one!
Tim, in case you’re still following the thread, you wrote:
I’m not sure what you mean by the odds not changing. Maybe you mean the probability that we picked the correct door initially. Then, you’re right, the probability that that door is the correct door does not change after Monty opens one of the doors.
When Monty opens another door revealing a goat, that tells us nothing about whether the car is behind our door or not, because Monty will never open a door revealing a car. If we initially picked the correct door, Monty will reveal a goat. If we initially picked the wrong door, Monty will reveal a goat. Therefore, Monty’s revealing a goat tells us absolutely nothing about whether we initially picked the correct door. Before Monty opened a door, the probability that we picked the correct door was 1/3. Since Monty’s opening a door tells us nothing about whether our initial pick was correct, the probability that it is is still 1/3 after Monty opens a door.
However, if we initially picked the wrong door—and there is a 2/3 probability that we did—then by Monty revealing another losing door, Monty is telling us exactly where the car is, namely, under the remaining door.
So, there is a 1/3 chance that we picked the correct door initially, but a 2/3 chance that we did not, in which case the car is behind the last remaining door. Therefore, we should switch.
Jay
On my long, busy commute this week, I was thinking about this problem. What a coincidence. After reading this it finally is making sense. Focusing on the likelihood of the outcome and not the possible reality was the key for me.
When I pretended to be Monty, I have 2 out of 3 chances of having the car behind the 2 left-over doors. If I toss out the loser, I still have 2/3’s probability of having the door with the car. But the player still has only 1/3. AND I know where the car is, so I don’t open that door.
If I turn the game around, it makes sense.
Eureka!!!
LOL, I’m a smart person….so I think. It was really bugging me that I didn’t understand the Monty Hall problem. I’ve watched YouTube videos over and over. Even Scam School did an episode on it. When Brian explained it, the people in the video immediately understood. Why didn’t I? So it has been a nagging obsession that enters my conscious thoughts chronically ever since. What a relief! On to bigger problems! 😉 Thanks, Barb!
A good explanation, Barbara. As one who has dealt with mathematics all my working life, it took me a long time to come to terms with the fact that my gut feeling just wasn’t enough to solve this problem, and that the contestant really should switch when presented with this situation. Of course a switch still doesn’t guarantee a win.
The easiest way to get that one should always switch is to know that you most likely got your first pick wrong.
If you had 1000 doors with only 1 prize, and picked one, do you really expect you got it right? The chance you got it right is 1/1000 (0.1%), the chance you got it WRONG is 999/1000 (99.9%)! So, another chance might be kind of nice, especially since you will get a hint!
The do-over goes like this: if AFTER you picked your (likely wrong) door, ALL remaining WRONG doors BUT ONE are revealed, leaving you with your lousy (1/1000 chance) initial door and ONE other door.
Why would you NOT switch since the one you already picked is almost certainly (999/1000) wrong?
Alternative description of the game:
The former is equivalent to a game where you get to pick one door out of 1000, and then get to declare that you think you either got the guess right, or wrong initially. The answer is revealed and if your declaration was true, you win!
Step by step:
Pick 1 out of 1000 doors, only 1 has a prize. You then get to ASSERT:
option A) MY door has the prize. (i.e. I guessed the right door!)
option B) The prize is behind one of the remaining 999 doors. (i.e. I guessed the wrong door!)
Having picked between the two options, the correct door is revealed: if your declared option is true, you win.
To relate this to the original problem: “Switching” is equivalent to declaring option B. In the prior example 998 of the “other doors” are revealed first, but it is no different in terms of winning since switching just says “I was probably wrong on my initial guess”.
The same decision logic goes for only 3 total doors since the chance you initially pick the wrong door is still more likely to be wrong (2/3 chance your initial pick is wrong).
The 1,000 (or 100, or 10) door option is one I’ve heard several times today and I don’t really see how it allows people to see the problem differently. It doesn’t really reframe the problem.
Your description of the options is the same reframing I described in the post and in my last comment.
The many doors allows a person to think in 1-p terms rather than p terms, by making p vanishingly small. So they can be “sure” they have the wrong door and when given a choice it is more “obvious” they should switch.
As for your revised re-framing, the similarity to mine is coincidental since I didn’t see your 2nd post when I made mine… we are talking about the same stuff after all so naturally it would be similar.
How about this variation to show how a small ‘p’ could help make the decision more obvious to the average person who doesn’t “get it” as stated originally:
A twisted lottery game for one player
A 20 digit lottery number is randomly chosen and put into a sealed envelope which only the commissioner knows.
You pick a lottery number of 20 digits long and get a ticket in your name from the commissioner with your number imprinted on it.
The commissioner shows you a second ticket and declares that either yours or theirs matches the number in the sealed envelope, but you are given the option to swap ownership of the two tickets before the envelope is opened!
Do you keep your ticket or switch with the commissioner’s? The decision to switch is no different if the “lottery number” is from 1-3 instead of 20 digits.
I may have used different language in my comment, but my reframing of the problem as two options is central in the post. This could just mean that I did not communicate it clearly.
I understand the purpose of exaggerating the numbers. I simply don’t believe it helps many people to understand the problem because changing that one thing does not reframe the problem. I know that you think it prompts them to and you are not alone in that opinion. I just don’t share it.
Your “twisted lottery” scenario makes little sense to me. It doesn’t map to the Monty Hall Problem and I fail to see how it would help anyone understand that problem. I honestly think that the best way to be comfortable with the answer is to see it as two options rather than 3 (or 100 or 1000).
I’m surprised you don’t see how the lottery maps into the Monty Hall problem, with a lottery number between 1 and 3, it is equivalent in terms of probability. I would think you should see this easily based on your apparent understanding of the problem.
Here is how it maps
Note: As a garden path like strategy, you first present the 20 digit example so they can see the initial pick is almost certainly wrong, once switching in that game is ‘accepted’ you then repeat the game restricted to a lottery number that’s 1,2 or 3 (1-3) in order to map it directly into Monty Hall:
specifically
The lottery number (1,2 or 3) maps into doors 1,2 or 3.
The commissioner knows the winning number and hides it in the envelope maps into: Monty Hall knows which door has the car.
Your ticket maps into your chosen door.
The commissioner declares that he holds the only remaining potentially winning ticket leaving only his and your ticket: that maps into the revealing the “wrong” door leaving only 2 doors.
You have a choice between the 2 remaining doors, maps into the choice between commissioner’s ticket (the remaining unopened door) or your ticket (your door)
Your offer to swap ticket ownership, maps into the choice to “switch” doors.
The envelope is opened and the winning number is revealed, maps into the winning door is revealed.
The door you end with maps into the ticket you own.
Finally
I agree with you that the essence of the game is the choice between two things and not between more than two things.
I acknowledge you made that point in your reply to Tim, but in my follow ups I only tried to make the same worded differently. Based on Tim’s post my attempts were unsuccessful as well, since he states he still doesn’t get it.
The challenge as I see it is to present and describe an equivalent game that people would accept easily, free of the cognitive misdirection the wording of the initial problem creates. Then you just map the new game into Monty Hall, which I think I did above.
If I did the mapping incorrectly, please help me by pointing out where I went off the rails.
My solution is a lot shorter:
There is a 1/3 probability that your initial choice was correct, but there is a 2/3 probability that it was wrong, in which case you will win by switching doors. So switch.
For a real mind f***, try the Tuesday Birthday Problem: A man walks up to you on the street and says, “I have two children, one of whom is a son who was born on a Tuesday. What is the probability that my other child is also a son?”
Jay
I know it is a slight nit of wording, but maybe a more accurate way to phrase it might be “…but there is a 2/3 probability that it was wrong, hence you will have better chances of winning by switching doors. So switch”.
This way the explanation doesn’t rhetorically discount the feature that “always switching” actually looses 1/3 of the time.
jsfb wrote:
No. Your wording leaves out a key point in my solution, that the probability of winning by switching, given that the door you first picked was wrong, is 1.
Now why would that be useful thing to communicate when one is talking about a strategy for working with uncertainty?
The revised wording was specifically intended to remove that rather obvious statement of fact, namely that if you know what the right answer is, pick it! In the MTP or any like it, the contestant never knows the answer until the game is over.
I remember that one. 13/27 if I recall correctly.
The problem bases itself off of the “don’t double-count” aspect of sets, which is why the more generic version (not specifying day of week for either child, just probability of both boys given 1 is a boy) is 1/3 rather than 1/2.