Why the “Critical” in Critical Thinking
In an age in which many teens and young adults seem to equate criticism and not getting what they want with disrespect, it should not be surprising that some argue for unconditional positive regard in education and elsewhere. However, criticism is essential to gaining knowledge.
I am sure that most people have not thought much about why it’s called “critical thinking” and, when asked, would probably assume that “critical” refers to its importance (especially skeptics). However, they would only be partially correct. “Critical” means “crucial”, but it also refers to discriminating judgments. Critical thinking is a process in which we distinguish accurate information from inaccurate information and/or determine the best course of action given a set of possibilities.
The reason criticism is so important is a bit abstract, but it can be at least partially illustrated through the principle of falsification. Essentially, attempting to falsify a hypothesis is the best way to determine if it is likely to be true.
Most skeptics are familiar with the confirmation bias, which is the very strong human tendency to favor confirming information. We notice, remember, believe, and assign more weight to information that confirms what we already believe to be true than other information. What is discussed less often is how this bias extends to how we seek knowledge and test hypotheses. Humans tend to experiment to determine relationships in the world, but we do so in a confirmatory manner when a better approach is to attempt to falsify. That is, we tend to try this or try that to see what happens. However, the best test of a hypothesis is one in which the outcome tells us what is likely to be true by eliminating other possibilities. This is how science works most of the time and I think that we can agree that science works better than any other method.
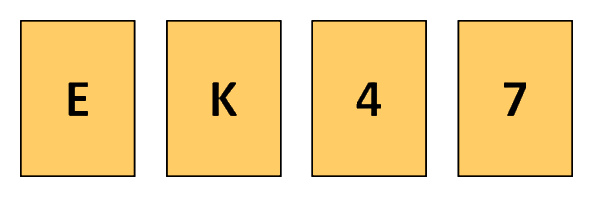
A good illustration of this human tendency is the Wason 4-Card Task. Fortunately, it is also a good way to explain why falsification is ideal.
In the Wason 4-Card Task (A.K.A. the Wason Selection Task), participants are given the following problem:
There are four cards in front of you, each with a letter on one side and a number on the other side. The rule is: If there is a vowel on one side of a card, then there must be an even number on the other side.
Which cards must be turned over to determine if the rule holds true? (How many cards, minimum, and which ones?)
The most popular answers in this task are the E and 4 cards or just the E card. This demonstrates an approach to hypothesis testing which is confirmatory in nature. That is, we search for examples of the first condition, then confirm that the second condition is met. This is similar to how most people deal with other types of questions, such as whether or not a pill reduces headache pain. How would you find out? Should you take the pill when you have headache pain, then judge the pill effective if the pain is gone an hour later?
Unfortunately, this approach is not a very effective means of gaining knowledge. To understand why, let’s look at what we can learn from turning over each card.
| Card | Outcome | Rule? |
|---|---|---|
| E | Even Number | True in this case |
| Odd Number | Violated | |
| K | Even Number | Unknown (rule doesn’t apply) |
| Odd Number | Unknown (rule doesn’t apply) | |
| 4 | Vowel | True in this case |
| Consonant | Unknown (rule doesn’t apply) | |
| 7 | Vowel | Violated |
| Consonant | Unknown (rule doesn’t apply) |
Only the bold information tells us anything about whether the rule holds true or not and only in the cases in which it is violated do we learn something meaningful enough to draw a conclusion. The correct answer to the basic Wason Task is that both the E and 7 cards are required. The E card can confirm the rule, but what is important is that it, and the 7 card, have the ability to falsify it. Turning over the 4 card is unnecessary because the rule does not even apply unless it has been followed, therefore, we learn nothing interesting.
If my statement about is confusing, you are not alone. This task is one of the most well-studied in the field of cognitive psychology, yet why humans are so bad at it is still a bit of a mystery. One of the hypotheses is that people have a difficult time recognizing that the rule is not bi-directional. In other words, the rule is:
If there is a vowel on one side, there is an even number on the other side.
it is NOT:
If there is a vowel on one side, there is an even number on the other side and vice-versa.
However, when conditional statements like this are made, we often assume that they are bi-directional unless we have context which tells us otherwise. For example, rules like these provide context which suggests more than what is stated:
If it is Monday, then the banks are open.
If I buy a ticket, I will win something in the raffle.
Because we have schemas that tell us that banks are open on weekdays (at least), we understand that the reverse of the first conditional (If the banks are open, then it is Monday) is not necessarily true. In the second conditional, our knowledge of how raffles work tells us that a raffle ticket must have been purchased if the author won something in it. In each case, however, we are not evaluating the statements on their own merit. We introduce information from our knowledge base. The problem with this kind of reasoning is that we assume that our knowledge is accurate.
When these statements are included in arguments, we draw conclusions based, at least in part, on our current understanding of the world, which could be wrong.
One example that I often used in class illustrates how strong this bias can be and how it affects our ability to determine cause and effect relationships. Given the following argument, students are asked to judge whether the argument is valid or invalid. They are reminded that “valid” refers only to whether the argument is logically sound and not whether the statements within it are true (truth is a separate property):
Major Premise: If I learn a lot, I will get a good grade on the test.
Minor Premise: I got a good grade on the test.
Conclusion: Therefore, I learned a lot.
On its surface, the argument appears valid. However, it is not. There is nothing in the major premise to indicate that learning is the only way to get a good grade on the test – that learning is required for a good grade. It merely states that learning will guarantee one. Unfortunately, some dedicated students who have successfully used flash cards and other rehearsal techniques in courses in which memorization is helpful – introductory courses with multiple-choice exams and so forth – will assume that this method of studying equates to learning. When they fail in a more rigorous upper-division course in which conceptual understanding is necessary, they will be unlikely to attribute that failure to their study methods.
Going back to the example of how to determine if a pill takes away your headache pain, the method most people follow is to turn over the E card and nothing else. If your headache pain does not go away (outcome: an odd number), then you will know that the pill doesn’t work. However, what if the headache does go away? Is it possible that headaches go away on their own? Could taking the pill induce a placebo effect? What you need is to design an experiment in which you can eliminate all other possibilities (headaches go away by themselves, placebo effects, etc.). What you need to do is set the pill up to fail. If the headache goes away when it should (turning over the E card and finding an even number) AND it does not go away when it should not (turning over the 7 card and finding a consonant), then we can conclude that the pill worked.
The confirmational approach is like asking a psychic to predict the flip of a coin, but only counting the times in which the psychic was correct. This is an excellent way to find out if they have supernatural powers, but only if you also know the rate at which they are incorrect. When skeptics test psychics, they compare the outcome to what would be expected by chance. If they can consistently outperform blind guessing, the only logical conclusion is that they must not be guessing. To eliminate alternative explanations, skeptics ensure that the psychic is not receiving information from other sources such as body language cues.
Now, what does all of this have to do with criticism?
What science does, both in single studies and as a general process, is eliminate incorrect hypotheses. In general, scientists come up with likely hypotheses and theories based on what we are reasonably certain is true (as many as humanly possible), then eliminate them until only one remains. We eliminate them by finding faults with them, by demonstrating that they can’t be true (or are highly unlikely to be true).
Critical thinking works this way, too. The most effective process of evaluating information is one which looks for faults, inconsistencies, and weaknesses. Applying critical thinking to plans and ideas, otherwise we waste resources and time as well as risk harm. After we have completed a project, even a successful one, analysis should not focus on “what we did right”. We can’t know why we succeeded without comparisons to similar situations in which we failed. Focusing on what we think is good is like counting the “hits” and ignoring the “misses”.