Statistical Interactions

Basically, an interaction is when the effect of one factor (input variable) on the dependent variable (output variable) differs among levels of another factor.

For example, in a pain relief drug trial, one factor is “dose” and another factor is “gender”. The dependent variable is “headache pain” (measured on a scale of 0 to 50). We can look at the findings by showing the means for each group in a table like this:

	Male	Female
Placebo	30	10
50mg	10	30

If compare the “marginal means”, we can see that the average pain score for women was 20 and the average pain score for men was 20. There is no difference in headache pain between men and women. Likewise, the drug appears to have no effect on headache pain.

However, if we had stopped there, we would be missing some important findings. There is an interaction between gender and dose on headache pain. If we graph the means of each group, we can see it clearly: men have more headache pain than women unless they take the drug. There are simple effects of dose for both men and women, but the effects “wash out” one another. The result is no main effect of dose or gender. If you did not examine gender, it would appear that your drug did not work; if you did not study drug dose, you would see no difference between men and women. Examining the interaction allows us to see that the drug works – for men – AND that it causes pain in women.

This is called a “pure interaction” because there are no main effects, but there is an interaction.

More commonly seen, however, when effects occur in both (or all) conditions, but they are stronger in one condition than another. Also fairly common is an effect in one condition (or for one group), but no effect at all in another. For example, what if our same pain study resulted in the following means:

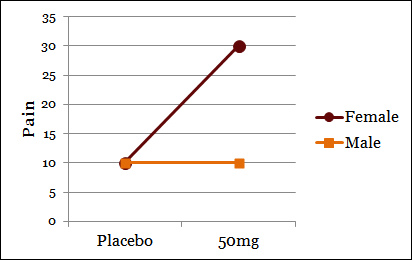
	Male	Female
Placebo	10	10
50mg	10	30

For men, there is no effect of the drug on headache pain. The drug causes pain in women, who would otherwise have the same amount of pain as men.

To recap, an interaction is when the effect of one variable differs among levels of another variable. When interactions are seen among continuous variables (variables with a range of values, as opposed to categories), they look a little different, but the meaning is basically the same. In the last example, difference in pain between men and women (the male average was 10, the female average was 20) are driven by the interaction with the drug.

ICBS Everywhere